The circumference of a circle of radius $r$ is $2\pi r$. This well known formula is taken up here from the point of view of similarity. It is important to note in this task that the definition of $\pi$ already involves the circumference of a circle, a particular circle.
In order to show that the ratio of circumference to diameter does not depend on the size of the circle, a similarity argument is required. Two different approaches are provided, one using the fact that all circles are similar and a second using similar triangles. This former approach is simpler but the latter has the advantage of leading into an argument for calculating the area of a circle.
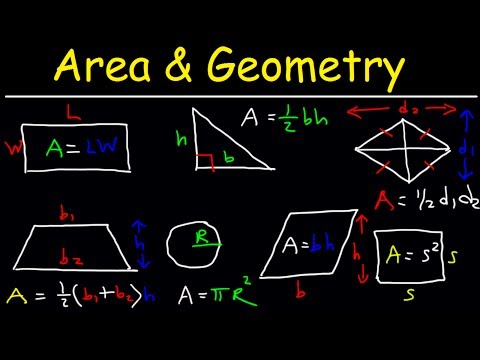
As with triangles and rectangles, we can attempt to derive formulas for the area and "perimeter" of a circle. Calculating the circumference of a circle is not as easy as calculating the perimeter of a rectangle or triangle, however. Diameter is the line that separates the circle into two equal parts and is also equal to twice the radius. A circle is a fundamental shape that is measured in terms of its radius. In geometry or mathematics, a circle can be defined as a special variety of ellipse in which the eccentricity is zero and the two foci are coincident.
This first argument is an example of MP7, Look For and Make Use of Structure. The key to this argument is identifying that all circles are similar and then applying the meaning of similarity to the circumference. The second argument exemplifies MP8, Look For and Express Regularity in Repeated Reasoning. Here the key is to compare the circle to a more familiar shape, the triangle. The first solution requires a general understanding of similarity of shapes while the second requires knowledge of similarity specific to triangles. The circle is divided into 16 equal sectors, and the sectors are arranged as shown in fig.
The area of the circle will be equal to that of the parallelogram-shaped figure formed by the sectors cut out from the circle. Since the sectors have equal area, each sector will have an equal arc length. The red coloured sectors will contribute to half of the circumference, and blue coloured sectors will contribute to the other half. If the number of sectors cut from the circle is increased, the parallelogram will eventually look like a rectangle with length equal to πr and breadth equal to r. The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae.
A circle is a closed curve formed by a set of points on a plane that are the same distance from its center. The area of a circle is the region enclosed by the circle. The area of a circle is equals to pi (π) multiplied by its radius squared. For those having difficulty using formulas manually to find the area, circumference, radius and diameter of a circle, this circle calculator is just for you. The equations will be given below so you can see how the calculator obtains the values, but all you have to do is input the basic information.
In above program, we first take radius of circle as input from user and store it in variable radius. Then we calculate the circumference of circle using above mentioned formulae and print it on screen using cout. In this image, you can see 16 sectors, including 8 green and 8 blue ones.
The green highlighted sectors represent the circle's half circumference while the other half of circumference is represented by blur highlighted ones. By increasing the number of the sectors cut from the circle, the parallelogram will change into a rectangle. The length of the rectangle would b equal to πr with a width equal to r. In this method, we divide the circle into 16 equal sectors. The sectors are arranged in such a way that they form a rectangle. All sectors are similar in area, so hence all sectors' arc length would be equal.
The circle's area would be the same as the area of the parallelogram shape or rectangle. We use this formula to measure the space which is occupied by either a circular plot or a field. In this article today, we will discuss the area of circle definition, the area of a circle equation, its circumference and surface area in detail. Cover the circle with concentric circles of "r" radius. After dividing the circle along the designated line shown in the above figure and spreading the lines, the outcome will be a triangle.
The base of the triangle will be equivalent to the circumference of the circle, and its height will be identical to the radius of the circle. Below is the formula calculation for the same. Students beginning geometry can expect to encounter problem sets that involve calculating the area and circumference of a circle.
You can solve these problems as long as you know the circle's radius and can do some simple multiplication. If you learn the value of the constant π and the basic equations for a circle's properties, you can quickly find the area or circumference of any circle. The perimeter of circle is nothing but the circumference, which is equal to twice of product of pi (π) and radius of circle, i.e., 2πr.
We have discussed till now the different parameters of the circle such as area, perimeter or circumference, radius and diameter. Let us solve some problems based on these formulas to understand the concept of area and perimeter in a better way. When the length of the radius or diameter or even the circumference of the circle is already given, then we can use the surface formula to find out the surface area.
The surface is represented in square units. Fill the circle with radius r with concentric circles. After cutting the circle along the indicated line in fig. 4 and spreading the lines, the result will be a triangle. The base of the triangle will be equal to the circumference of the circle, and its height will be equal to the radius of the circle. This area is the region that occupies the shape in a two-dimensional plane.
Now we will learn about the area of the circle. So the area covered by one complete cycle of the radius of the circle on a two-dimensional plane is the area of that circle. Now how can we calculate the area for any circular object or space?
In this case, we use the formula for the circle's area. In technical terms, a circle is a locus of a point moving around a fixed point at a fixed distance away from the point. Basically, a circleis a closed curve with its outer line equidistant from the center. The fixed distance from the point is the radius of the circle. In real life, you will get many examples of the circle such as a wheel, pizzas, a circular ground, etc. Now let us learn, what are the terms used in the case of a circle.
Formula For Area Of A Circle With Circumference Hence, the concept of area as well as the perimeter is introduced in Maths, to figure out such scenarios. But, one common question that arises among most people is "does a circle have volume? Since a circle is a two-dimensional shape, it does not have volume. So, we don't have the volume of a circle.
In this article, let us discuss in detail the area of a circle, surface area and its circumference with examples. Fizzywoz - If you look at examples #1-#4 at the end of the article you can see how numbers are plugged into the equation. You will usually just plug in a known radius into the equation to figure out the circumference or you may plug in a known circumference to determine the radius. Let me know if you have any other questions. A circle is divided into congruent sectors . The sectors are pulled out of the circle and are arranged as shown in the middle diagram.
The length across the top is half of the circumference. When placed in these positions, the sectors form a parallelogram. The larger the number of sectors that are cut, the less curvy the arcs will appear and the more the shape will resemble a parallelogram. As seen in the last diagram, the parallelogram ca be changed into a rectangle by slicing half of the last sector and placing it to the far left. From point B, on the circle, draw another circle with center at B, and radius OB. The intersections of the two circles at A and E form equilateral triangles AOB and EOB, since they are composed of 3 congruent radii.
Extend the radii forming these triangles through circle O to form the inscribed regular hexagon with 6 equilateral triangles. Is called the circumference and is the linear distance around the edge of a circle. The circumference of a circle is proportional to its diameter, d, and its radius, r, and relates to the famous mathematical constant, pi (π).
I am going to discuss these axioms in a moment, but first let me show how Claim follows. But by Axiom 1 the length of the arc $PBQ$ is greater than $PQ$, while it follows from Euclid III.2 that $OB$ is greater than $OA$. Applying symmetry, this implies Claim in this case, and ought to suggest how the reasoning goes in general. Finding the radius is not always easy, especially if you don't have the circle's center. You can calculate the area using the diameter instead.
The same formula applies as above, but you need first to calculate the radius of the circle. Simply divide the diameter by 2 to get the radius. Only a mathematician can genuinely understand the practical importance of formulas for calculating area, radius, diameter, or circle circumference.
While most people think that formulas have no practical use, they are critical factors in many everyday life routines. When we have the length of the diameter or the radius or the circumference of the circle, we can find the surface area of the circle by using the surface area formula. This surface area of the circle is represented in terms of square units.
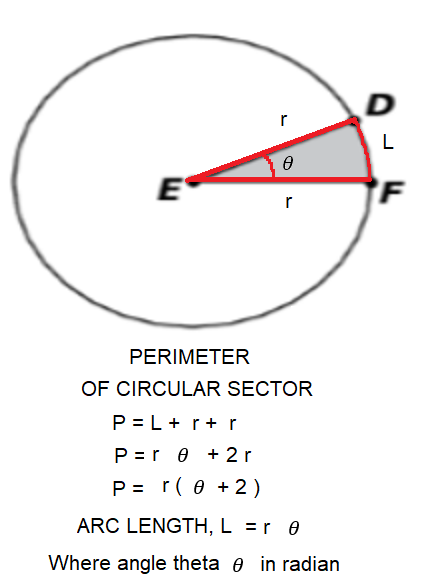
The perimeter of a closed figure is known to be the length of its total boundary. When it comes to the circles, the perimeter is called by a different name. It is referred to as the 'circumference' of the given circle. This circumference is known as the total length of the boundary of the given circle. If we open the circle and form a straight line, the length of the straight line that we get is the circumference.
For defining the circumference of a circle, we need to know a term called 'pi'. Consider the circle shown below having its centre at O and radius r. A circle is known as a closed plane geometrical shape. Technically, it is the locus of a point that moves around a fixed point at a fixed distance that is away from that point. A circle is basically a closed curve that has its outer line at an equal distance from the centre.
This fixed distance from the central point is known as the radius of the circle. In our day to day life, we often see many examples like a pizza, wheel, etc. Let us learn about these terms in regards to a circle. Π is simply a ratio between the diameter, d of a circle and it's circumference. In other words, a circle that has a diameter of 1 or a radius of 1/2 will have a circumference of π. Π is conveniently also the ratio of r squared to the area of the circle, meaning that a circle with radius 1 will have an area of π.
Let's take a look at some of your questions. To recall, the area is the region that occupied the shape in a two-dimensional plane. In this article, you will learn the area of a circle and the formulas for calculating the area of a circle.
Since area is a measure of two dimensions, you always report area in square units like square inches or square feet . This is especially important when calculating the area of a circle for an assignment since an answer without correctly reported units is likely incorrect or incomplete. Say you're trying to calculate the area of a circle with a radius of 3 inches. You would multiply 3 times 3 to get 9, and multiply 9 times π. Also note that when you multiply inches by inches, you get square inches, which is a measurement of area instead of length.
When you are doing calculations involving a circle, you frequently use the number π, or pi. Pi is defined as being equal to the circumference of a circle -- the distance around that circle -- divided by its diameter. However, you don't need to memorize this formula when working with π, since it is a constant.
The value of π is always the same, 3.14. Calculating either the circumference or area of a circle requires knowing the circle's radius. A circle's radius is the distance from the center of the circle to any point on the edge of the circle. Radius is the same for all points on a circle's edge. One of your problems might give you diameter instead of radius and ask you to solve for area or circumference. A circle's diameter is equal to the distance across the center of the circle, and is equal to the radius times 2.
So, you can convert diameter to radius by dividing the diameter by 2. For example, a circle with a diameter of 8 has a radius of 4. As we know, the area of circle is equal to pi times square of its radius, i.e. π x r2. To find the area of circle we have to know the radius or diameter of the circle. A perimeter of closed figures is defined as the length of its boundary. When it comes to circles, the perimeter is given using a different name.